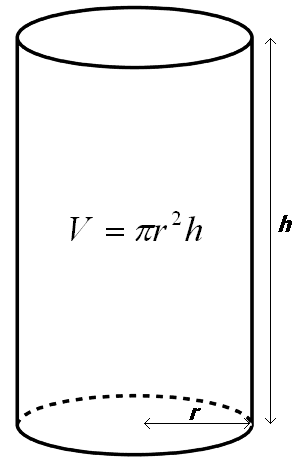El volumen es el espacio que ocupan los cuerpos.
El volumen es el espacio que ocupan los cuerpos.Los cuerpos geométricos existen en el espacio y son por lo tanto objetos que tienen tres dimensiones (ancho, alto y largo) limitados por una o más superficies. Si todas las superficies son planas y de contorno poligonal, el cuerpo es un poliedro. Si el cuerpo no está limitado por polígonos, sino por superficies curvadas recibe el nombre de cuerpos redondos.
La fórmula para calcular el volumen de un cuerpo depende de su forma.
Para medir el volumen de un cuerpo se utilizan unidades cúbicas (u^3).
Ahora te presentaremos formulas para obtener el volumen de:
Cubo
Prisma
Cilindro
Piramide
Cono
Esfera
Tambien te proporcionamos 2 ejercicios resuletos para un mejor entendimiento:
Ejercicio 1
Ejercicio 2
Ademas estos ejercicios nos ayudan a entender que el volumen de los prismas y las pirámides se determina aplicando fórmulas, en las cuales se relaciona su longitud, altura y anchura, mientras que en el cilindro y el cono se relacionan el radio y la altura.
Para finalizar nos gustaria pesentarte algunos otros terminos sobre el volumen:
- En matemáticas el volumen es una medida que se define como los demás conceptos métricos a partir de una distancia o tensor métrico.
- En física, el volumen es una magnitud física extensiva asociada a la propiedad de los cuerpos físicos de ser extensos, que a su vez se debe al principio de exclusión.
- En escultura y pintura, la manera de tratar la tridimensionalidad de las masas.
- En escultura, se le llama volumen a una estructura formal tridimensional, así como también volumen a las partes componentes del todo escultórico, cuando éstas tiene el carácter de masas.
- En pintura, el volumen es la sugerencia de peso y masa lograda por medios estrictamente pictóricos que reflejan características tridimensionales.
- En arquitectura, el conjunto exterior de un edificio, que encierra el espacio interior.
Y en especial la vision que la Teoria del Diseño tiene acerca del volumen:
- El recorrido de un plano en movimiento se convierte en volumen, tiene posición en el espacio, esta limitado por planos y obviamente en un diseño bidimensional el volumen es ilusorio.
- Cada visión representa sólo una parte del objeto total, pero el pensamiento gestáltico nos induce a interrelacionar las caras para obtener una percepción del volumen como forma visual integrada.
- La toma de conciencia de que cada cara o parte del volumen fluye y se continúa en las demás es decisiva para el acto de diseñar.
- Muchos no consideran el volumen como uno de los elementos básico del diseño. Lo consideran como una consecuencia de aplicar formas, líneas y colores.

- La línea basta para crear volumen. A medida que añadamos sombras, tonos, y perspectiva aumentamos la sensación de volumen. Cuanto más realista es una imagen, mas volumen tendrá.